TO ALCOHOL SOCIOLOGY HOME PAGE
Citation: Roizen, R., and Milkes, J., "The Strange Case of the Jellinek Formula's Sex Ratio," Journal of Studies on Alcohol 41:682-692, 1980.
The Strange Case of the Jellinek Formula's Sex Ratio1Ron Roizen and John Milkes
SUMMARY. The historical development of the Jellinek formula is reviewed and it is concluded that the formula's male:female ration of 5 : 1 or 6 : 1 is unjustified.
IN THE UNITED STATES between about 1947 and 1958 the determination of the sex ratio of the prevalence of alcoholism was more or less exclusively the province of the Jellinek formula. It consistently produced male : female ratios between 5 : 1and 6 : 1. The authoritativeness of the formula began to decline after 1958, however, and along with that decline came a reduction in the authority of its sex ratio. But no other sex-ratio estimate as come along to occupy the position it once held. Thus the current literature on alcoholism's sex ratio often handles the topic by merely presenting a variety of different estimates ranging from lows of 1 : 1 to highs of 15 : 1 or 20 : 1, depending on the source (e.g., 1-3). Authors presenting such ranges rarely choose among them, with the result that there is no consensual answer to the question, What is the sex ratio of alcoholics in the United States today?
In the absence of a clearly superior estimate, the Jellinek formula has kept up a visible presence in the sex-ratio literature, though it is not the predominating influence it once was. Beckman (4), for example, in her review of the literature on alcoholism among women, relied on the formula's sex-ratio estimate. Keller (5) suggested that since the major criticisms of the Jellinek formula have not questioned its sex-ratio determination, the ratio should still be regarded as valid in spite of the formula's other difficulties. In fact, there has been no careful look at the formula's sex-ratio calculation in the critical literature.
The Formula's Basic Structure
The Jellinek formula is a method for estimating the prevalence of alcoholism from liver cirrhosis mortality data. Its underlying rationale is quite simple: the formula, in essence, asks, How big must the pool of living alcoholics be in order to provide a certain number of cirrhosis deaths among alcoholics in a given year?
The approach of the Jellinek formula derives from the principle that there are two equally good ways of calculating the number of cirrhosis deaths experienced by alcoholics in a given year: (1) the number of alcoholics alive in a given year can be multiplied by the probability that an alcoholic will die of cirrhosis in that year, or (2) the total number of cirrhosis deaths in a given year can be multiplied by an estimate of the proportion of alcoholics among all cirrhosis deaths.
In the notation of the formula, then, the-se two ways to calculate the liver cirrhosis deaths among alcoholics can be expressed as follows: A * K = P * D, where A = the total number of alcoholics alive in a given year, K = the probability that an alcoholic will die of cirrhosis in that year, D = the total number of liver cirrhosis deaths in that year and P = the proportion of liver cirrhosis deaths contributed by alcoholics. Or, that the total number of alcoholics alive in a given year multiplied by the probability an alcoholic will die of cirrhosis in that year is equal to the total number of cirrhosis deaths in that year multiplied by the proportion of cirrhosis deaths contributed by the alcoholic population.
Solving this equation for A, the total number of alcoholics alive in a given year, we get, A = PD/K. This is the form of the original Jellinek formula. Again, in words, it tells its that the number of alcoholics alive in a given year is equal to the number of cirrhosis deaths multiplied by the proportion of cirrhosis deaths contributed by alcoholics, divided by the probability an alcoholic will die of cirrhosis in a given year.
But this equation is not the formula's most recent form. When the formula was first being worked out the word "alcoholic" had a rather different meaning for Jellinek from what it acquired in the years to come (6). In the early 1940s the term "alcoholic" referred to a person with a physical illness related to his drinking. Thus, for example, an "alcohol addict" was not necessarily an "alcoholic" unless he or she also manifested some alcohol-related physical illness. Also, someone who was not dependent on alcohol but nevertheless had acquired a physical illness related to drinking would qualify as an alcoholic. The original Jellinek formula was calculated with this definition of alcoholism in mind.
By the late 1940s and early 1950s, though, the term "alcoholism" had taken on a broader meaning for Jellinek: it came to include persons who did not necessarily have an alcohol-related physical illness. Thus, it was necessary for the calculation of the old formula to be increased by a factor that expressed the ratio of all alcoholics (whether or not they had a physical illness) to alcoholics with a physical illness. In the new nomenclature this was termed the ratio of "alcoholics with and without complications" to "alcoholics with complications." The term "alcoholic with complications," then, took on the meaning the term "alcoholism" alone had had in the early 1940s. As a result of this change, the new formula was written, A = (PD/K) * R, where R = the ratio of all alcoholics to alcoholics with complications.
Because P (the proportion of cirrhosis deaths contributed by alcoholics), K (the probability of death from cirrhosis in a given year among alcoholics) and R (the ratio of all alcoholics to alcoholics with complications) were all seen as constants in the Jellinek formula, only D (the number of cirrhosis deaths reported in a given year) varied. Thus the formula's estimate of the prevalence of alcoholism was essentially a linear function of the number of cirrhosis deaths. In fact, the formula might as easily have been originally written as A = D * S, where A = the total number of alcoholics alive in a given year, D = the total number of liver cirrhosis deaths in that year and S = the constant PR/K, in the original formula. Or, even more simply, it could have originally been written, A = 242D, or 242 living alcoholics for every cirrhosis death, according to the original constants.
The Formula's Sex Ratio
Roughly twice as many men as women die of liver cirrhosis in the United States annually. Since the Jellinek formula relies on cirrhosis mortality, one would expect that its alcoholism prevalence estimates for the two sexes would lie roughly in the same proportion, namely, two men alcoholics for every one woman alcoholic. But this is not the case. As we mentioned above, Jellinek formula calculations have consistently reported ratios between five and six men to one woman alcoholic. This is because Jellinek used slightly different formulas for the calculation of alcoholism prevalence among men and women. The structure of the formula and the constants K and R were the same for both sexes, but Jellinek suggested different values for P (the proportion of cirrhosis deaths contributed by alcoholics) in the formulas for men and women. He suggested, in the World Health Organization (7) description of the formula, that 51.5% of male cirrhosis deaths but only 17.7% of female cirrhosis deaths were contributed by alcoholics. Thus, the fact that the formula's alcoholism prevalence sex ratio is roughly three times greater than the sex ratio of cirrhosis mortality in the United States is attributable to this difference in P values.
Why Were Jellinek's Male and Female P Values Different?
Jellinek never published a detailed account of his derivations of
the male and female P values, so we can only guess at their source. In the original form of the Jellinek formula, only a P value for both sexes combined was calculated (6, 8). That calculation was made on the basis of trend data on cirrhosis mortality, comparing death rates before and after national Prohibition in the United States. Jolliffe and Jellinek (8) noted that U.S. cirrhosis mortality, after a period of gradual decline between 1900 and 1915, dropped sharply between 1916 and 1920. The nadir of this decline, they argued, was coincident with the period of the greatest enforcement and effectiveness of Prohibition. After 1920 cirrhosis mortality stayed relatively low, and then rose sharply after 1933 and Prohibition's repeal. The authors reasoned that the 1916-20 decline in cirrhosis mortality was probably due to the drying up of alcohol supplies, and thus could be regarded as a measure of alcohol's contribution to the over-all cirrhosis rate.Jolliffe and Jellinek (8) also noted trends in both tuberculosis mortality and general mortality, in order to check for the possibility that cirrhosis mortality had declined as part of a general decline in mortality between 1916 and 1920. Both rates, general and tuberculosis mortality, in fact did show declines over the period, but both continued declining in the period 1932-40 whereas cirrhosis mortality rose dramatically in that period. It followed that, although part of the 1916-20 decline in cirrhosis mortality might be credited to a decrease in general mortality, most of the fall in the cirrhosis rate was properly assigned to the decline in alcohol consumption. In order to estimate the fraction of cirrhosis mortality attributable to alcohol above ana beyond any decrease in the population's general mortality, Jolliffe and Jellinek subtracted the 1916-20 decrease in general mortality (a 7.1% decline) from the 1916-20 decrease in cirrhosis mortality (a 42.2% decline). In this way they arrived at an estimate of the net contribution of alcohol to cirrhosis mortality: 42.2% (the rate of decline in cirrhosis) minus 7.1% (the rate of decline in the general mortality, a rough measure of improvement in health generally) gave 35.1%. That is to say, 35% of cirrhosis mortality was contributed by alcoholics. Certainly this method was not suitable for anything more than a rough estimate and was open to a number of serious criticisms, though we will not consider them here (9).
If Jellinek used the same method for calculating sex-specific P values, then we would expect that the vital statistics on sex-specific rates of cirrhosis mortality between 1916 and 1920 were quite different, the men's rate of decline being much sharper than the women's. Table I shows the sex-specific rates for liver cirrhosis and for general mortality in 1916 and 1920.
As Jellinek's P estimates suggested, Table 1 shows that the male cirrhosis rate did fall more sharply than the female rate between 1916 and 1920. But the difference is not nearly as large as Jellinek's P values required. Moreover, Jolliffe and Jellinek (8) reduced the percentage decline in the cirrhosis mortality rates by the rate of decline in general mortality. The same calculation (i.e., subtracting from the 33.8% decline in female cirrhosis the 1.9% decline in female general mortality, and subtracting from the 42.7% decline in male cirrhosis the 9.3% decline in male general mortality) produces almost equal net declines in cirrhosis mortality for males and females: net male decline, 33.4%; net female decline, 31.9%. On the basis of these statistics, then, Jellinek's sex-specific values should have been roughly equal; and they hardly justified separate P values or separate calculations of the Jellinek formula for the two sexes.
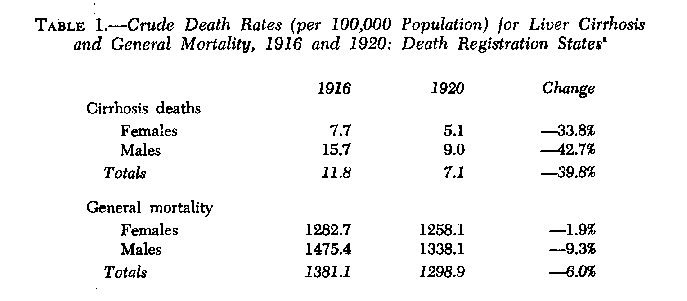 aSource: Linder and Grove (10, p. 259). The total (i.e., combined-sexes) rates of cirrhosis and general mortality in 1916 and 1920 do not agree exactly with the rates reported by Jolliffe and Jellinek (8): they reported a 42.2% decline in cirrhosis mortality (versus a 39.8% decline) and a 7.1% decline in general mortality (versus a 6.0% decline). As a result, the over-all P value Jolliffe and Jellinek computed, 35.1 or 35%, is slightly higher than the rate which would be computed from our data, 33.8 or 34%. This difference in rates stems from differences in the "reporting areas" from which the death rates were drawn. Jolliffe and Jellinek drew their rates from a 1939 Vital Statistics Report in which rates were based on the "Registration Area of the United States," whereas our rates, drawn from Linder and Grove, are based on the U.S. "Death Registration States." The former includes a few cities in states not included in the registration system. Thus, following Jolliffe and Jellinek's example as closely as we could, it would have been preferable for us to compute the sex-specific P values on the same base Jolliffe and Jellinek used, but it was not possible to find sex-specific population estimates for the Death Registration Area and thus sex-specific death rates could not be computed on that base. There is no reason to suspect, however, that this difference could account for the divergence in Jellinek's and our own sex-specific P values.
aSource: Linder and Grove (10, p. 259). The total (i.e., combined-sexes) rates of cirrhosis and general mortality in 1916 and 1920 do not agree exactly with the rates reported by Jolliffe and Jellinek (8): they reported a 42.2% decline in cirrhosis mortality (versus a 39.8% decline) and a 7.1% decline in general mortality (versus a 6.0% decline). As a result, the over-all P value Jolliffe and Jellinek computed, 35.1 or 35%, is slightly higher than the rate which would be computed from our data, 33.8 or 34%. This difference in rates stems from differences in the "reporting areas" from which the death rates were drawn. Jolliffe and Jellinek drew their rates from a 1939 Vital Statistics Report in which rates were based on the "Registration Area of the United States," whereas our rates, drawn from Linder and Grove, are based on the U.S. "Death Registration States." The former includes a few cities in states not included in the registration system. Thus, following Jolliffe and Jellinek's example as closely as we could, it would have been preferable for us to compute the sex-specific P values on the same base Jolliffe and Jellinek used, but it was not possible to find sex-specific population estimates for the Death Registration Area and thus sex-specific death rates could not be computed on that base. There is no reason to suspect, however, that this difference could account for the divergence in Jellinek's and our own sex-specific P values.
On the basis of this exercise, then, it seems that Jellinek formula estimates of alcoholism's sex ratio should indeed have produced ratios directly proportional to the cirrhosis mortality sex ratio. In other words, it seems that Jellinek either was not justified in establishing the sex-specific P values he used or he used a modified method, one differing in some respects from the one used to calculate the over-all or combined-sexes P.We have reviewed a number of different modifications Jellinek might have introduced into his calculation method, but none seem likely to account for the sex-specific P's he recommended. In fact, it seems more likely that Jellinek simply adjusted the values of the sex-specific P's to fit conventional thinking (namely, a 6 : I ratio) about the relative prevalence of alcoholism among men and women in the contemporary United States. Or, put the other way around, a formula which at that time generated a 2 : 1 sex ratio (men to women) might have seemed to run against conventional wisdom much more than would have an adjustment of the sex-specific estimates of the proportions of cirrhosis deaths contributed by alcoholics.
Incidentally, if Jellinek had wished to create sex-specific P estimates that would generate roughly a 6 : 1 sex ratio, then the male P would have to be about 3 times greater than the female P, and the average of the two P's would have to be .35, the number calculated for the over-all P value in the 1941 paper (8). This fact makes for an intriguing explanation of another mystery surrounding the Jellinek formula's P values. In Jellinek's 1951 discussion of the formula (7) the procedure for calculating the over-all P value was described and in the same way that it was described in 1941. Thus, the over-all P value of the 1951 description should have the same value as the over-all P value of the 1941 description (8). But, in fact, they do not. In the 1951 description Jellinek suggested sex-specific P's of .515 for men and .177 for women. These two values taken together will produce an over-all P value of .40 (and not .35) because cirrhosis is twice as prevalent among men as among women. Because the men's rate of cirrhosis is double the women's rate, the contribution of men alcoholics to all cirrhosis mortality must be given roughly twice the weight of the contribution of women alcoholics. And, therefore, for the over-all cirrhosis rate the P value will come out to .40.
Had Jellinek overlooked this, he would have required that the male and female P values produce a simple average of about .35. In fact, the two P values he suggested have a simple mean of .35. Popham (11) was the first to point out that Jellinek's sex-specific P values implied a .40 and not a .35 value for the over-all cirrhosis rate, though Popham seems to have concluded that Jellinek merely had revised his estimate of the over-all value upward. No account of an increase in the over-all P value was ever published by Jellinek. We, of course, are suggesting that the .40 value was created by Jellinek who overlooked the fact that it was not the simple mean but a weighted mean of the sex-specific P values that should equal .35.
Revision of the P Values in 1952
In 1952 Jellinek (12) proposed new values for the P's, increasing the male value from .515 to .628 and the female value from .177 to .216. This change was not based on new data or on a new method for calculating P per se. In 1949 U.S. Vital Statistics adopted the Sixth Revision of the International Lists of Diseases and Causes of Death, which did not alter the diagnostic criteria for the various sorts of cirrhosis classifications, but it did alter the rules for coding the primary cause of death when multiple causes are mentioned. Jellinek described the circumstances as follows (12, pp. 216-217):
"Because of the great artificial changes in trends brought about by the 'Sixth Revision,' the National Office of Vital Statistics undertook a comparability study of mortality statistics . . . in order to establish comparability ratios. A 10-per-cent sample of the deaths in the 2-year period 1949-1950 was used in that study, and 64 selected causes of death (among them cirrhosis of the liver) were tabulated once according to the Fifth Revision of the International Lists of Causes of Deaths . . . and once according to the Sixth Revision of the International Lists. For deaths from cirrhosis of the liver the study of this sample yielded the following statistics: According to the Fifth Revision, deaths from cirrhosis of the liver numbered 3448, but according to the Sixth Revision they numbered 2818, a decrease of 630 due to the revised system of recording.
"In this large sample the effect of the 'Sixth Revision' was, thus, to reduce the reported number of deaths from cirrhosis of the liver by 18 per cent. On the basis of this sample the National Statistical Office proposes a 'comparability ratio' of 0.82 (2818/3448)."In short, if the actual number of cirrhosis deaths remained constant across two test years, the first employing the Fifth Revision and the second employing the Sixth Revision, the apparent deaths from cirrhosis would decline by 18%. Thus, in order to offset this "paper" decline in the cirrhosis rate, data from years in which cirrhosis mortality was calculated on the basis of the Sixth Revision would have to be multiplied by a constant to make up for the "undercount" attributable to the revision itself. This constant was 1.22 in the case of cirrhosis deaths. Jellinek multiplied the men's and women's P's, .515 and .177, by 1.22 in order to compensate for the Sixth Revision, producing the new Ps of .628 for men and .216 for women.
The revision of the P values in 1952 is noteworthy in this paper because it was essentially a technical modification to compensate for a change in mortality reporting and did not significantly alter the sex ratio of the formula.
The Consequences of Our Calculation
If, in fact, the P values for men and for women should have been the same, both calculated at about .33, then the sex ratio for alcoholism in the Jellinek formula should not have hovered around 5 or 6 : I but instead around 2 : 1 or the sex ratio of cirrhosis mortality, whatever it happened to be. Estimates for men have been too high, about 55% higher than the appropriate estimate. Implied in this is that Jellinek formula estimates for men should be multiplied by a factor of 0.65 in order to calculate the corrected prevalence number or prevalence rate. Estimates of alcoholism among women, on the other hand, have been too low, or only about 53% of the appropriate estimate. This implies that published estimates should be multiplied by a factor of 1.88. These modifications have an impact on the total prevalence of alcoholism as well: Jellinek's sex-specific P values implied an over-all P value of about .40 (instead of the .35 that Jolliffe and Jellinek had originally calculated in 1941). If the true P value for the two sexes had emerged as .33 in both, then the over-all P value, as well, would have been estimated at .33. It follows that total prevalence estimates for alcoholism, which incorporated the implicit .40 value for P, were about 20% higher than the appropriate estimate, and should be multiplied by 0.83 in order to correct them.
We mentioned that the change in P values suggested by Jellinek in 1952 (12) was not intended to reflect a true change in his estimate of the contribution of alcoholism to cirrhosis mortality, but instead was just a technical change introduced in order to compensate for the "undercount" of cirrhosis deaths brought about by the Sixth Revision. If Jellinek had been using the P value we have calculated, .33, for both sexes, he would have increased it by the 1.22 factor, thus bringing that P to .403. The correction factors (0.65 for men, 1.88 for women and 0.83 for total) express the proportional relationship between Jellinek's P values and the P value we have suggested based on our own analysis. These proportional relations, of course, are not affected by introducing an "undercount factor" of 1.22 into both Jellinek's values and our own. Thus, the correction factors would apply equally well to Jellinek formula estimates for times before and after the 1949 revision.
Concluding Comments
Though we have suggested a revised value for P and correction factors to be applied to Jellinek formula estimates of the past, we should stress here that these recommendations are made in order to clarify the formula's history and not to reform it or correct the formula for present-day use. The critical literature on P had convincingly shown that P should not have been set at a constant value but made a variable figure anyway (9, 13, 14). Making P a variable, moreover, will move the sex ratio from roughly 2 : 1 to roughly 3 : 1, because the putative alcohol contribution to cirrhosis rises as the cirrhosis death rate rises, and since men have higher cirrhosis mortality rates than women, men's alcoholic cirrhosis rate will also be higher than women's.
Despite this caveat, there may still be a risk that some readers will use our "correction factors" to arrive at correct, or at least more correct, prevalence estimates. But there are so many other difficulties with the formula that we think it is better to discourage its use altogether rather than to leave open the implication that the correction factors should be used. Also, in the present climate of considerable political interest respecting the prevalence of alcoholism among women, it would be unfortunate to encourage readers to believe that the ratio is smaller than it probably really is. This would be to repeat Jellinek's error in the other direction.2
Our central conclusion is rather that Jellinek would not have arrived at the sex-specific P values he later published (7) by following the approach Jolliffe and he (8) used in calculating an over-all P value for the sexes combined. If one follows the procedure described in the 1941 paper (8) for each sex, then the resulting P values for the two sexes are nearly the same, or about .33, or one-third of cirrhosis deaths. This conclusion, in turn, leads us to suggest that the history of prevalence estimation in the U.S.A. might have shown sex ratios of roughly 2 : 1 rather than sex ratios varying from 5 : 1 to 6: 1 during the period of the Jellinek formula's hegemony in the prevalence field, if indeed the formula would have established its hegemony in its corrected form.
1 From the the School of Public Health, University of California, Berkeley, 1816 Scenic Avenue, Berkeley, California 94720.2 We are indebted to an anonymous JOURNAL reviewer for suggesting this paragraph's content.
ACKNOWLEDGMENTS.--This work was supported by an Alcohol Research Center grant form the National Institute on Alcohol Abuse and Alcoholism. We thank Joan Friedman, Kaye Fillmore, Oriana Kalant and an anonymous Journal reviewer for their help and suggestions.
Received for publication: 13 August 1979. Revision: 11 February 1980.
1. LINDBECK, V. L. The woman alcoholic; a review of the literature. Int. J. Addict. 7: 567-580, 1972. REFERENCES
2. GOMBERG, E. S. The female alcoholic. Pp. 603-636. In: TARTER, R. E. and SUGERMAN, A. A., eds. Alcoholism; interdisciplinary approaches to an enduring problem. Reading, Mass.; Addison-Wesley; 1976.
3. SCHUCKIT, M. A. and MORRISSEY, E. R. Alcoholism in women; some clinical and social perspectives with an emphasis on possible subtypes. Pp. 5-35. In: GREENBLATT, M., and SCHUCKIT, M. A., eds, Alcoholism problems in women and children. New York; Grune & Stratton; 1976.
4. BECKMAN, L. J. Women alcoholics; a review of social and psychological studies. J. Stud. Alcohol 36: 797-824, 1975.
5. KELLER, M. The definition of alcoholism and the estimation of its prevalence. Pp. 310-329. In: PITTMAN, D. J. and SNYDER, C. R., eds. Society, culture, and drinking patterns. New York; Wiley; 1962.
6. HAGGARD, H. W. and JELLINEK, E. M. Alcohol explored. Garden City, N.Y.; Doubleday, Doran; 1942.
7. WORLD HEALTH ORGANIZATION. EXPERT COMMITTEE ON MENTAL HEALTH. Report on the first session of the Alcoholism Subcommittee. Annex 2. Jellinek estimation formula. (WHO Tech. Rep. Ser., No. 42.) Geneva; 1951.
8. JOLLIFFE, N. and JELLINEK, E. M. Vitamin deficiencies and liver cirrhosis in alcoholism. Pt 4. Cirrhosis of the liver. Q. J. Stud. Alcohol 2: 544-583, 1941.
9. POPHAM, R. E. Indirect methods of alcoholism prevalence estimation; a critical evaluation. Pp. 294-306. In: POPHAM, R. E., ed. Alcohol and alcoholism. Toronto; University of Toronto Press; 1970.
10. LINDER, F. E. and GROVE, R. D. Vital statistics rates in the United States 1900-1940. Washington, D.C.; U.S. Govt Print. Off.; 1943.
11. POPHAM, R. E. The Jellinek alcoholism estimation formula and its application to Canadian data. Q. J. Stud. Alcohol 17: 559-593, 1956.
12. JELLINEK, E. M. The estimate of the number of alcoholics in the U.S.A. for 1949 in the light of the Sixth Revision of the International Lists of Causes of Death. Q. J. Stud. Alcohol 13: 215-218, 1952.
13. BRENNER, B. Estimating the prevalence of alcoholism; toward a modification of the Jellinek formula. Q. J. Stud. Alcohol 20: 255-260, 1959.
14. SEELEY, J. R. Estimating the prevalence of alcoholism; a critical analysis of the Jellinek formula Q. J. Stud. Alcohol 20: 245-254, 1959.